Topic What percent is equivalent to 3/8: The fraction 3/8 can be easily converted into a percentage by dividing 3 by 8, which equals 0.375. To convert this to a percentage, you simply multiply it by 100. Therefore, 3/8 is equivalent to 37.5%. This skill of converting fractions to percentages is important in understanding fractions and their relation to whole numbers. Mastering this skill can help students better grasp mathematical concepts.
Table of Content
- What percent is equivalent to 3/8?
- How do you convert the fraction 3/8 into a percentage?
- What is the numerical equivalent of 3/8 as a percentage?
- YOUTUBE: Convert 3/8 to a Percent
- What is the step-by-step method to convert 3/8 into a percentage?
- Why is understanding fractions and their percentage equivalents important in mathematics?
- What are some other examples of fractions and their equivalent percentages?
- Can you explain the concept of dividing a whole into 100 parts to calculate percentages?
- How can converting fractions to percentages help in real-life situations?
- Are there any shortcuts or tricks to quickly convert fractions to percentages?
- Are there any common mistakes or misconceptions when converting fractions to percentages?
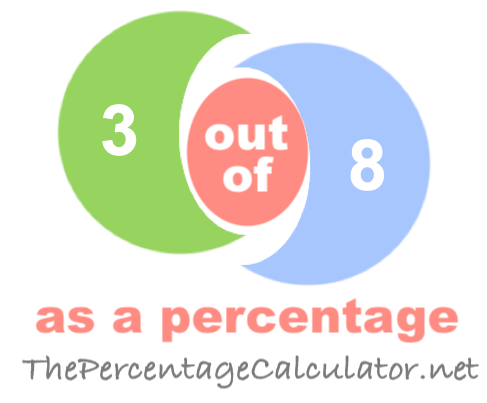
What percent is equivalent to 3/8?
To find the percentage equivalent of 3/8, you can follow these steps:
1. First, divide the numerator (3) by the denominator (8): 3 ÷ 8 = 0.375.
2. This gives you the decimal equivalent of 3/8.
3. To convert this decimal into a percentage, multiply it by 100: 0.375 * 100 = 37.5.
4. Therefore, 3/8 is equivalent to 37.5%.
So, 37.5% is the percentage equivalent of 3/8.
How do you convert the fraction 3/8 into a percentage?
To convert the fraction 3/8 into a percentage, you can follow these steps:
1. Divide the numerator (top number) of the fraction by the denominator (bottom number): 3 ÷ 8 = 0.375.
2. Multiply the result by 100 to convert the decimal into a percentage: 0.375 Ã 100 = 37.5.
Therefore, 3/8 as a percentage is 37.5%.
What is the numerical equivalent of 3/8 as a percentage?
To find the numerical equivalent of 3/8 as a percentage, you can follow these steps:
1. Start by dividing the numerator (the top number) by the denominator (the bottom number): 3 ÷ 8 = 0.375.
2. Next, multiply the result by 100 to convert the decimal to a percentage: 0.375 * 100 = 37.5.
Therefore, 3/8 is numerically equivalent to 37.5% as a percentage.
Convert 3/8 to a Percent
\"Discover the power of conversion with our latest video! Learn how to effortlessly convert different units, measurements, and even currencies with our step-by-step guide. Say goodbye to confusion and embrace the ease of conversion with us!\"
What is the step-by-step method to convert 3/8 into a percentage?
To convert 3/8 into a percentage, follow these steps:
Step 1: Divide the numerator (3) by the denominator (8) - 3 ÷ 8 = 0.375
Step 2: Multiply the result by 100 to convert it into a percentage - 0.375 Ã 100 = 37.5%
Therefore, 3/8 is equivalent to 37.5% as a percentage.
Why is understanding fractions and their percentage equivalents important in mathematics?
Understanding fractions and their percentage equivalents is important in mathematics for several reasons:
1. Comparative analysis: Fractions and percentages allow us to compare quantities. By understanding their relationship, we can easily determine which quantity is larger or smaller. This skill is necessary when making decisions based on measurements, such as comparing prices or quantities of items.
2. Real-world applications: Fractions and percentages are used in various real-life situations, such as calculating discounts, sales tax, or interest rates. Being able to convert between fractions and percentages allows us to work with these concepts more easily and accurately.
3. Problem-solving: Many mathematical problems involve fractions and percentages. By understanding their equivalents, we can solve problems more efficiently. For example, when solving word problems that involve finding a percentage of a quantity, knowing how to convert fractions to percentages or vice versa helps to simplify the problem-solving process.
4. Interpreting data: Fractions and percentages are commonly used to represent data, such as statistical reports, surveys, and probability. Understanding their equivalence allows us to interpret data accurately and draw meaningful conclusions. For example, when reading a pie chart, knowing that each sector represents a percentage allows us to understand the proportions of different categories.
5. Communication and clarity: Fractions and percentages are commonly used in communication, both in math and in other subjects. Being able to express ideas in fractions or percentages helps in conveying information precisely and concisely. It also allows for efficient communication of mathematical concepts and calculations among mathematicians, scientists, and researchers.
In summary, understanding fractions and their percentage equivalents is crucial in mathematics as it enables us to compare quantities, solve problems, interpret data, communicate effectively, and apply mathematical concepts to real-life situations.
_HOOK_
What are some other examples of fractions and their equivalent percentages?
Sure! Here are some examples of fractions and their equivalent percentages:
1. 1/4 is equivalent to 25%. To find the percentage, you divide 1 by 4 and then multiply by 100. So, 1/4 = (1/4) * 100 = 0.25 * 100 = 25%.
2. 2/5 is equivalent to 40%. To find the percentage, you divide 2 by 5 and then multiply by 100. So, 2/5 = (2/5) * 100 = 0.4 * 100 = 40%.
3. 3/10 is equivalent to 30%. To find the percentage, you divide 3 by 10 and then multiply by 100. So, 3/10 = (3/10) * 100 = 0.3 * 100 = 30%.
4. 1/2 is equivalent to 50%. To find the percentage, you divide 1 by 2 and then multiply by 100. So, 1/2 = (1/2) * 100 = 0.5 * 100 = 50%.
5. 5/8 is equivalent to 62.5%. To find the percentage, you divide 5 by 8 and then multiply by 100. So, 5/8 = (5/8) * 100 = 0.625 * 100 = 62.5%.
These are just a few examples of fractions and their equivalent percentages. Remember that to find the percentage, you divide the numerator of the fraction by the denominator, then multiply by 100.
Finding Equivalent Fractions for 3/8
\"Master the fascinating world of equivalent fractions in just a few minutes! Our engaging video breaks down the concept into simple, bite-sized explanations, making it easy for you to understand and apply in various math problems. Join us on this educational journey and unlock the magic of equivalent fractions!\"
3/8 as a Percentage
\"Unveiling the secrets behind percentages in our captivating video presentation! Whether you\'re a student looking to ace your exams or an aspiring business professional seeking to enhance your analytical skills, this video is a must-watch. Learn how to calculate percentages, solve practical scenarios, and gain the confidence you need to conquer any task involving percentages!\"
Can you explain the concept of dividing a whole into 100 parts to calculate percentages?
Sure! When we calculate percentages, we are essentially finding a proportion or ratio out of 100. To do this, we divide the number or quantity we want to express as a percentage by the total amount and then multiply by 100.
In the context of the fraction 3/8, we want to determine what percentage it represents. To do this, we divide 3 by 8, which gives us 0.375. This means that 3/8 is equal to 0.375 as a decimal.
Next, we multiply 0.375 by 100 to convert it to a percentage. Multiplying by 100 shifts the decimal point two places to the right, resulting in 37.5. Therefore, the equivalent percentage for 3/8 is 37.5%.
To summarize the steps:
1. Divide the numerator (the top number of the fraction) by the denominator (the bottom number of the fraction) to get a decimal.
For example, 3 ÷ 8 = 0.375.
2. Multiply the decimal by 100 to convert it to a percentage.
For example, 0.375 Ã 100 = 37.5.
By dividing a whole into 100 parts, we are essentially expressing a fraction or a portion of that whole as a percentage out of 100. This allows us to easily compare different quantities or determine the proportion of a certain amount in relation to the whole.
How can converting fractions to percentages help in real-life situations?
Converting fractions to percentages is a practical skill that can be useful in many real-life situations. Here are a few examples:
1. Shopping and Sales: When shopping, you often come across discounts or sales where prices are given in percentages. By knowing how to convert fractions to percentages, you can easily determine the discounted price. For instance, if there is a 3/8 discount on an item, you can convert it to a percentage (37.5%) and calculate the reduced price.
2. Cooking and Baking: Recipes sometimes require measurements that are given in fractions. Converting these fractions to percentages can help you adjust ingredient amounts easily. For example, if a recipe calls for 3/8 cup of sugar and you need to make a smaller or larger batch, you can convert it to a percentage (37.5%) and adjust the measurement accordingly.
3. Financial Planning: Understanding percentages is crucial in financial planning and budgeting. Calculating interest rates, discounts, sales tax, or investment returns often involves converting fractions to percentages. For example, if you are comparing two investment options with different interest rates expressed as fractions, converting them to percentages can help you evaluate which option may yield a higher return.
4. Statistics and Data Analysis: Percentages are widely used in presenting statistical data. Converting fractions to percentages allows you to better understand and interpret numerical information. Whether you are analyzing survey results, market reports, or population statistics, knowing how to convert fractions to percentages helps in grasping the significance of the data.
Overall, converting fractions to percentages is a valuable skill in various aspects of daily life. It enables better understanding, calculation, and comparison of data, measurements, and values, thus facilitating decision-making and problem-solving in practical situations.
Are there any shortcuts or tricks to quickly convert fractions to percentages?
Yes, there are a few shortcuts and tricks you can use to quickly convert fractions to percentages.
1. First, note that a percentage is a way to express a fraction out of 100. To convert a fraction to a percentage, you need to multiply the fraction by 100.
2. To convert the fraction 3/8 to a percentage, you can multiply 3/8 by 100:
(3/8) * 100 = (3 * 100) / 8 = 300/8 = 37.5
3. So, 3/8 is equivalent to 37.5% as a percentage.
This method works for any fraction you want to convert to a percentage. Just multiply the fraction by 100 and simplify if necessary.
Another shortcut you can use is to divide the numerator (top number) of the fraction by the denominator (bottom number) and then multiply by 100.
For example, to convert 5/6 to a percentage, divide 5 by 6 and multiply by 100:
(5/6) * 100 = (5 * 100) / 6 = 500/6 â 83.33
So, 5/6 is approximately equivalent to 83.33% as a percentage.
These shortcuts can save you time in converting fractions to percentages, but it\'s always important to understand the underlying concept of how percentages relate to fractions.
Are there any common mistakes or misconceptions when converting fractions to percentages?
When converting fractions to percentages, there are a few common mistakes or misconceptions that people might have:
1. Not multiplying by 100: To convert a fraction to a percentage, you need to multiply it by 100. This is because a percentage is a fraction out of 100. For example, to convert 3/8 to a percentage, you would calculate (3/8) * 100.
2. Forgetting to simplify the fraction first: Before converting a fraction to a percentage, it is important to simplify the fraction as much as possible. In the case of 3/8, it is already simplified. However, if the fraction is not simplified, it can lead to incorrect percentage values.
3. Not rounding the percentage properly: When converting a fraction to a percentage, it is common practice to round the percentage to a certain number of decimal places. The number of decimal places depends on the desired level of accuracy. For example, 3/8 as a decimal is 0.375, but as a percentage, it is commonly rounded to 37.5%.
4. Misunderstanding the concept of percentage: Some people may have difficulty understanding what a percentage actually represents. A percentage is a proportion or a fraction of a whole, where the whole is represented by 100. So, 3/8 as a percentage can be thought of as \"what percent is 3 out of 8 of a whole hundred\". In this case, the answer is 37.5%.
It is important to double-check calculations and understand the concept of percentages to avoid making these common mistakes or misconceptions.
_HOOK_